This week's lab is a bit of a potpourri of topics
...
:
Quicksort Algorithm
Variable Argument Lists
Two Visitor Styles
Binary Search Algorithm
Insertion into a Doubly-linked list
| Anchor | ||||
|---|---|---|---|---|
|
Quicksort
Quicksort is the most common sorting algorithm in use today. In light of its technological impact, it's good to know how it works.
...
On average, quicksort will be faster than mergesort because the partitioning process of breaking the set into "smaller" and a "larger" subsets is less computationally expensive than mergesort's generalized merge operation. On the other hand, if the set is pathological, e.g. it's already sorted, Quicksort will degenerate into a O(N*N) behavior while mergesort will always be O(N*log(N)).
Here 's a very basic implementation of Quicksort in an imperative coding style:are some links to some animations of the Quicksort algorithm (all imperative/procedural code):
- http://www.animatedrecursion.com/intermediate/quicksort.html
- http://www.cs.auckland.ac.nz/software/AlgAnim/qsort.html
- http://pages.stern.nyu.edu/~panos/java/Quicksort/index.html
Here's a very basic implementation of Quicksort in an imperative coding style:
| Code Block |
|---|
import java.util.*;
class QuicksortBasic implements QuickSort {
public ArrayList<Integer> sort(ArrayList<Integer> a) {
if (a.isEmpty()) return new ArrayList<Integer>();
ArrayList<Integer> |
| Code Block |
import java.util.*;
class QuicksortBasic implements QuickSort {
public ArrayList<Integer> sort(ArrayList<Integer> a) {
if (a.isEmpty()) return new ArrayList<Integer>();
ArrayList<Integer> left = new ArrayList<Integer>();
ArrayList<Integer> mid = new ArrayList<Integer>();
ArrayList<Integer> right = new ArrayList<Integer>();
for (Integer i : a)
if ( i < a.get(0) )
left.add(i); // Use element 0 as pivot
else if ( i > a.get(0))
right.add(i);
else
mid.add(i);
ArrayList<Integer> left_s = sort(left);
ArrayList<Integer> right_s = sort(right);
left_s.addAll(mid);
left_s.addAll(right_s);
return left_s;
}
}
|
...
The split operations is just the partitioning of the array into two parts, one smaller than the pivot and one larger than the pivot. The split operation corresponds to the "partition" function that many Quicksort implementations identify. The join operation is simply a no-op because the two sorted subsets are disjoint and contiguous, so they are already in order.
...
===================================================================================================================
| Anchor | ||||
|---|---|---|---|---|
|
Variable Argument Lists
We discussed this before in lab and lecture, but it's worth revisiting to make sure everyone understands it.
...
(Note: there are more efficient ways of writing this method, but I wanted to show you several features at once)
Wiki Markup
The following are all valid calls to the above method:
...
===================================================================================================================
| Anchor | ||||
|---|---|---|---|---|
|
A A Tale of Two Visitors
You were shown two different styles of writing visitors, with and without input parameters. Why two different techniques?
...
Who's "right"? That depends on where you stand and what's important to you. Perhaps neither. You choose what's right for what you're trying to do at that moment. There is no gospel, only defensible but non-absolute positions. . Perhaps neither. You choose what's right for what you're trying to do at that moment. There is no gospel, only defensible but non-absolute positions.
===================================================================================================================
| Anchor | ||||
|---|---|---|---|---|
|
Binary Search in a Sorted Array
The recursive technique used to find a value in a sorted array is very useful in many situations.
Consider the following sorted array of values:
[1, 2, 4, 7, 10, 11, 12, 13, 20, 25, 27, 28, 30]
Supposed you're give a value, x, what's the fastest way to either find that value in the array or determine if it is not present?
The trick is to use the same technique many people use to find a name in a phonebook, a technique called a "binary search" because it is continually making the searched space smaller by a factor of two:
- Open the book in the middle
mid = (max+min)/2(min, max and mid are the page numbers here) - If the name you want is on that page, you're done.
- If the name is before the names where you opened the book, re-open the book halfway on the smaller side and repeat the process.
- If the name is after the names where you opened the book, re-open the book halfway on the larger side and repeat the process.
For the above array, we would look for the number 11 by doing the following:
- min = 0, max = 13, so mid = 6 ==> so look at the #12 (min, max and mid are indices into the array here)
- min= 0, max = 6, and 11 < 12, so look at mid = (6+0)/2 = 3, i.e. the #7.
- min= 3, max = 6, and 11 > 7, so look at the mid = (6+3)/2 = 4, i.e. the #10
- min = 4, max = 6 and 11>10 so look at the mid=(4+6)/2 = 5, i.e. the #11
- min = 5, max = 6, there's only one element left and since 11 = 11, we found it!
Here's some Java code to do the same:
| Code Block |
|---|
/**
* Uses binary search to find x in the given array within the given min (inclusive) and max (exclusive) bounds.
* returns true if found, false otherwise.
*/
boolean find(int x, int[] anArray, int min, int max) {
if(0 >= (max-min) {
return false; // safety catch, should never hit this.
}
else if(1 == (man-min)) { // only one element to look at
return anArray[min] == x; // return true is equal, false otherwise
}
else { // still looking
int mid = (max+min)/2; // integer arithmetic will round down.
if(anArray[mid] <= x) { // careful here, need to make sure midpoint is included if x = anArray[mid]
return find(x, anArray, mid, max); // recur with smaller bounds = upper half of the original bounds.
}
else {
return find(x, anArray, min, mid); // recur with smaller bounds = lower half of the original bounds
}
}
}
|
Such as search is very fast, running in O(log N) time because you are reducing the size of the space by a constant multiplicative factor every time your recurse.
One way to look at what is going on here is to think of the sorted array as already being in the form of a binary search tree, where each mid-point is the top node of a sub-tree. All the above algorithm is doing is walking down from the top of the binary search tree, i.e the path 12 => 7 => 10 => 11.
| No Format |
|---|
12
/ \
7 25
/ \ / \
2 10 13 28
/ \ \ \ / \
1 4 11 20 27 30
|
It is a very useful notion to conceptually view an array as a tree. This enables one to leverage the power of recursive data structures with the speed and compactness of an array.
===================================================================================================================
| Anchor | ||||
|---|---|---|---|---|
|
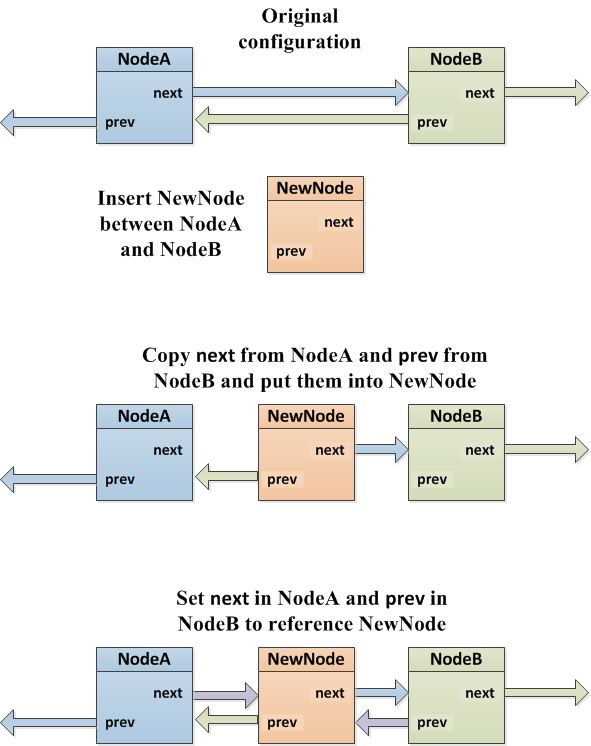
Insertion into a Doubly-linked List
Inserting a node into a doubly-linked list, ala BiList, isn't difficult, but it does take care to make sure that one has the right values for the node references at any given moment. Here's a pictoral explanation of the process: